Avogadro's Number Law

Avogadro's Number Lab Report
Avogadro's Number Law Office
Avogadro's Gas Law
Avogadro's Number Law Enforcement
Avogadro's Law Problems

Contrary to the beliefs of generations of chemistry students, Avogadro’s number—the number of particles in a unit known as a mole—was not discovered by Amadeo Avogadro (1776-1856).
Avogadro’s law, a statement that under the same conditions of temperature and pressure, equal volumes of different gases contain an equal number of molecules. This empirical relation can be derived from the kinetic theory of gases under the assumption of a perfect (ideal) gas.

Avogadro’s Number. In tribute to Avogadro, also the number of particles (atoms, molecules, ions or other particles) in 1 mole of a substance, 6.022×10 23, was named after Avogadro as the Avogadro constant or Avogadro number.The Avogadro constant is one of the seven SI base units and represented by N A. The Avogadro’s Law can be used for comparing the same substance under two different.

05th Apr 2019 @ 11 min read

Avogadro's law is also known as Avogadro's hypothesis or Avogadro's principle. The law dictates the relationship between the volume of a gas to the number of molecules the gas possesses. This law like Boyle's law, Charles's law, and Gay-Lussac's law is a specific case of the ideal gas law. This law is named after Italian scientist Amedeo Avogadro. He formulated this relationship in 1811. After conducting the experiments, Avogadro hypothesized that the equal volumes of gas contain the equal number of particles. The hypothesis also reconciled Dalton atomic theory. In 1814 French Physicist Andre-Marie Ampere published similar results. Hence, the law is also known as Avogadro-Ampere hypothesis.

Statement

For an ideal gas, equal volumes of the gas contain the equal number of molecules (or moles) at a constant temperature and pressure.

In other words, for an ideal gas, the volume is directly proportional to its amount (moles) at a constant temperature and pressure.

Explanation

As the law states: volume and the amount of gas (moles) are directly proportional to each other at constant volume and pressure. The statement can mathematically express as:

Replacing the proportionality,

where k is a constant of proportionality.

The above expression can be rearranged as:

The above expression is valid for constant pressure and temperature. From Avogadro's law, with an increase in the volume of a gas, the number of moles of the gas also increases and as the volume decreases, the number of moles also decreases.

If V₁, V₂ and n₁, n₂ are the volumes and moles of a gas at condition 1 and condition 2 at constant temperature and pressure, then using Avogadro's law we can formulate the equation below.

Let the volume V₂ at condition 2 be twice the volume V₁ at condition 1.

Therefore, with doubling the volume, the number of moles also gets double.

The formation of water from hydrogen and oxygen is as follows:

$underset{1,text{mol}}{ce{H2O}}$}' alt='Water reaction'>

In the above reaction, 1 mol, (n_H₂) of hydrogen gas reacts with a ¹⁄₂ mol (n_O₂) of oxygen gas to form 1 mol (n_H₂O) of water vapour. The consumption of hydrogen is twice the consumption of oxygen which is expressed below as:

Let say, 1 mol of hydrogen occupies volume V_H₂, a ¹⁄₂ mol of oxygen occupies V_O₂ and similarly for 1 mol of water vapour, volume V_H₂O. As we know from Avogadro's law, equal volumes contain equal moles. Hence, the relationship between the volumes is the same as among the moles as follows:

Avogadro's law along with Boyles' law, Charles's law and Gay-Lussac's forms ideal gas law.

Graphical Representation

The graphical representation of Avogadro's law is shown below.

The above graph is plotted at constant temperature and pressure. As we can observe from the graph that the volume and mole have a linear relationship with the line of a positive slope passing through the origin.

As shown in the above figure, the line is parallel to the x-axis. It means that the value of volume by mole is constant and is not influenced by any change in mole (or volume).

Both the above graphs are plotted at a constant temperature and pressure.

Avogadro's constant

The Avogadro's constant is a constant named after Avogadro, but Avogadro did not discover it. The Avogadro's constant is a very useful number; the number defines the number of particles constitutes in any material. It is denoted by N_A and has dimension mol⁻¹. Its approximate value is given below.

Molar Volume

Since Avogadro's law deals with the volume and moles of a gas, it is necessary to discuss the concept of molar volume. The molar volume as from the name itself is defined as volume per mole. It is denoted as V_m and having a unit of volume divided by a unit of mole (e.g. dm³ mol⁻¹, m³ kmol⁻¹, cm³ mol⁻¹ etc). From the ideal gas law, at STP (T = 273.15 K, P = 101 325 Pa) the molar volume is calculated as:

Limitation of Avogadro's law

The limitation are as follows:

The law works perfectly only for ideal gases.
The law is approximate for real gases at low pressure and/or high temperature.
At low temperature and/or high pressure, the ratio of volume to mole is slightly more for real gases compare to ideal gases. This is because of the expansion of real gases due to intermolecular repulsion forces at high pressure.
Lighter gas molecules like hydrogen, helium etc., obey Avogadro's law better in comparison to heavy molecules.

Real World Applications of Avogadro's Law

Avogadro's principle is easily observed in everyday life. Below are some of the mentioned.

Balloons

When you blow up a balloon, you are literally forcing the air from your mouth to inside the balloon. In other words, you are filling more moles of air in the balloon and it expands.

Tyres

Have you ever filled deflated tyres? If yes, then you are nothing but following Avogadro's law. When you pump air inside the deflated tyres at a gas station, the amount (moles) of gas inside the tyres is increased which increases the volume and the tyres are inflated.

Human lungs

When we inhale, air flows inside our lungs and they expand while when we exhale, the air flow from the lungs to surroundings and the lungs shrink. David axelrod twitter.

Laboratory Experiment to prove Avogadro's law

Objective

To verify Avogadro's law by estimating the amount (moles) of different gases at a fixed volume, temperature and pressure.

Apparatus

The apparatus requires for this experiment is shown in the above diagram. It consists of a U-tube manometer (in the diagram closed-end manometer is used, but opened-end manometer can also be used) as depicted in the figure, mercury, a bulb, a vacuum pump, four to five cylinders of different gases and a thermometer. Connect the all apparatuses as shown in the figure.

Nomenclature

V₀ is the volume of the bulb, which is known (or determined) before the experiment.
T is the temperature at which the experiment is performed, which can be determined from the thermometer (for simplicity take it as room temperature).
P is the pressure at which the experiment is performed, which can be determined from the difference in heights of mercury level in the manometer.
W₀ is the empty weight of the bulb, and it is known (or determined) before the experiment.
W is the filled weight of the bulb.
W_g is the weight of the gas inside the bulb.
M is the molar mass of the gas.

Procedures

Take a gas cylinder attached it the bulb setup and also attached the pump to the bulb setup. Care must be taken while attaching the apparatus to prevent any leakages of the gas.
First, close the knob of the gas cylinder and open the vacuum pump knob on the bulb. Evacuate the air filled in the system and by turning on the vacuum pump.
Once the bulb is emptied, close the vacuum pump knob and switch off the vacuum pump.
Start filling the bulb with the cylinder gas by opening the gas cylinder knob slowly until the desired difference in the mercury height is achieved. Note the height difference in the manometer. (The value of the height difference should be the same for all the readings.)
Close all the knobs, also close the connection between the bulb and the manometer to isolate the gas inside the bulb. Disassemble the bulb from the manometer.
Weigh the bulb on a weighing machine and note the reading down.
This finishes the procedure for the first gas. Repeat the same procedure for different gases.

Calculation

Calculate the weight of gas (W_g) in the bulb by subtracting the weight of empty bulb (W₀) from the weight of the filled bulb (W).

Then calculate the number of moles of the gas as:

The number of moles of all gases should be approximately equal within a small percentage of error. If this is true, then all the gases do obey the Avogadro's law.

If the experiment is performed at STP (T = 273.15 K, P = 101 325 Pa) , then we can also calculate the molar volume V_m as:

And its value should be close to 22.4 dm³ mol⁻¹.

Examples

Example 1

Consider 20 mol of hydrogen gas at temperature 0 °C and pressure 1 atm having the volume of 44.8 dm³. Calculate the volume of 50 mol of nitrogen gas, at the same temperature and pressure?

Graphql markdown problems. As from Avogadro's law at constant temperature and pressure,

Therefore, the volume is 112 dm³.

Example 2

There is the addition of 2.5 L of helium gas in 5.0 L of helium balloon; the balloon expands such that pressure and temperature remain constant. Estimate the final moles of gas if the gas initially possesses 8.0 mol.

The final volume is the addition of the initial volume and the volume added.

From Avogadro's law,

The final number of moles in 7.5 L of the gas is 12 mol.

Example 3

3.0 L of hydrogen reacts with oxygen to produce water vapour. Calculate the volume of oxygen consumed during the reaction (assume Avogadro's law holds)?

For the consumption of every one mole of hydrogen gas, half a mole of oxygen is consumed.

As per Avogadro's law, the volume is directly proportional to moles, so we can rewrite the above equation as:

1.5 L of oxygen is consumed during the reaction.

Associated Articles

If you appreciate our work, consider supporting us on ❤️ patreon.

9
cite
response

Copy Article Cite

Definitions and Formulas

Avogadro’s law states that the volume of any gas is proportional to the amount of gas in moles when the temperature and pressure remain constant. In other words, equal volumes of any gas contain the same number of molecules if the conditions do not change. Note that masses of the different gases will not be the same because they have different molecular masses. A balloon filled with helium will be 33 times lighter than a balloon filled with xenon gas.

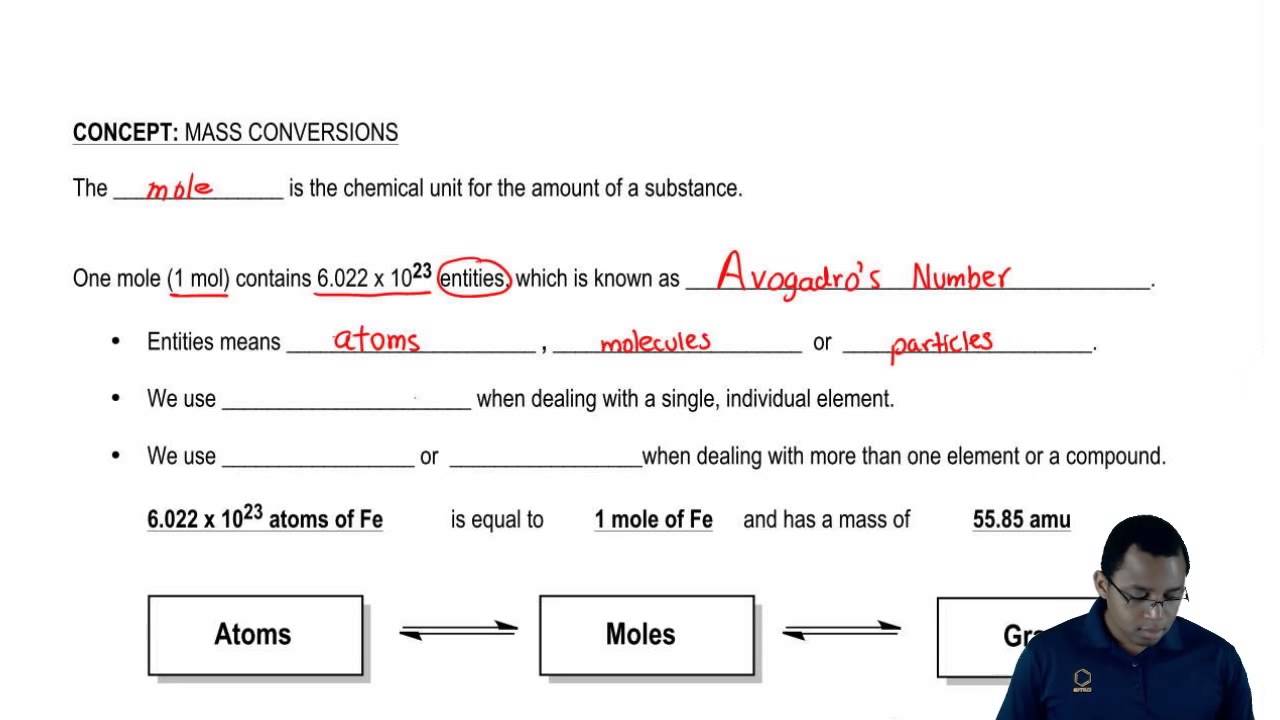
A mole is a measure of the quantity of a substance. A mole of a substance is defined as exactly 6.022 140 76 × 10²³ particles (atoms, molecules, ions, or electrons). A mole of a substance measured in grams is numerically equal to the average mass of one molecule of the compound, in unified atomic mass units. For example, one mole of oxygen with an atomic mass of 16 corresponds to 16 grams of this gas. One mole of an ideal gas at standard conditions occupies 22.4 liters. The number 6.022 140 76 × 10²³ is called the Avogadro constant.

A modern statement of Avogadro’s law states:

Avogadro's Number Lab Report

For a given mass of an ideal gas, its volume and amount in moles are directly proportional if the temperature and pressure maintained constant.

Mathematically, the law can be written as

where k is a constant depending on a given pressure and temperature. This means the ideal gas constant is the same for all gases.

Avogadro's Number Law Office

If we consider the pairing of variables at different states (initial and final) of the same process, we can write a proportion:

where V is the volume, n is the amount of substance in moles and the subscripts 1 and 2 refer to the initial and final states of a gas in a system. Any unknown term of this proportion can be found by means of cross-multiplication. For example, to find the initial volume V₁, we will write

History

An Italian scientist Amedeo Avogadro is best known for the Avogadro constant or Avogadro number, which only bears his name and was proposed by a French scientist Jean Perrin in 1909 and first calculated by an Austrian chemist and physicist Joseph Loschmidt (1865) and later by James Clerk Maxwell (1873). Unlike the Avogadro’s constant, Avogadro’s law was actually proposed by Amedeo Avogadro. It was the fourth empirical gas law and was published in 1811 after Boyle’s law (1662), Charles’s law (1787), and Gay-Lussac’s law (1808). Textbooks in French call this law La loi d'Avogadro-Ampère because it was independently formulated by a French scientist André-Marie Ampère in 1814.

It is noteworthy that during Avogadro’s lifetime, the discovery of his law went unnoticed due to criticism from influential chemists of that era — a Swedish chemist Jöns Jacob Berzelius and an English chemist John Dalton. They denied the possibility of the existence of diatomic molecules of simple substances. Only in 1860, the Karlsruhe Congress (the first international congress of chemistry) recognized the role of Avogadro.

Avogadro’s law, which is also called Avogadro’s principle or Avogadro’s hypothesis, only approximates the behavior of real gases because it applies only to an ideal gas. Real gases behave like an ideal gas only under conditions of low temperatures and pressures. At high temperatures and pressures, real gases do not behave in accordance with Avogadro’s law. Also, lighter gas particles of hydrogen, helium yield better results than heavier molecules.

Avogadro's Gas Law

Examples of Avogadro’s Law in Real Life Situations

Aerodynamics and Meteorology: Humid Air is Less Dense than Dry Air

Avogadro’s law is of great importance in aerodynamics with reference to engine thrust and wing lift. Dry air consists mostly of nitrogen and oxygen molecules, which weigh more than water molecules. This means that a given volume of moist air is lighter than the same volume of dry air. This is because lighter water vapor molecules present in the humid air “push out” oxygen molecules. At the same time, the number of molecules in a given volume of gas at the same temperature and pressure is the same regardless of its humidity. Humid air with water is less dense than dry air and consequently, it produced less wing lift force and less engine thrust. In conclusion, we have to note that this difference in density seems to be counterintuitive to many people (water is heavier than air!).

Air Balloons

Hydrogen and Helium balloons

Both hydrogen and helium gases are used in toy and weather balloons. They have the same temperature as surrounding air, almost the same pressure, and according to Avogadro’s law, the same number of molecules. At the same time, helium and hydrogen balloons can float because helium molecules and hydrogen atoms are much lighter than molecules of nitrogen and oxygen.

Hot Air Balloons

Hot air balloons float because the air in them is hotter than the air surrounding them. This hot air contains fewer molecules compared to the same volume of the surrounding air. The temperature and pressure of the air inside and outside the balloon are approximately the same and the balloon flotation is due to it has fewer molecules of gases in the air and thus it is lighter than the surrounding air.

A Ball

When you blow up a ball, its volume increases because you add more molecules. When, however, its valve is not working properly, some of the air leaks our and its volume decreases.

Lungs

Our body needs oxygen to live. It needs oxygen for thinking, moving, digesting food, and all other biochemical processes. When these processes happen, living tissues need oxygen for oxidation, which, in turn, is primarily used for rendering energy that is used for useful purposes. Carbon dioxide is produced as a waste product of this oxidation processes.

Avogadro's Number Law Enforcement

Our body needs ventilation to remove carbon dioxide and provide oxygen. Breathing (or ventilation) is the process of moving air into our lungs and out of them to provide gas exchange, which is mostly bringing in oxygen and removing carbon dioxide. When we breathe, inhaled air contains by volume 21% oxygen, 78% nitrogen, and very small amounts of other gases including carbon dioxide, water vapor, and noble gases. The exhaled gas contains by volume up to 5% of carbon dioxide, which is about a 100-fold increase over the inhaled amount of carbon dioxide.

We breathe because of Avogadro’s and other gas laws. When we inhale air (this is called inspiration), our lungs expand and more gas molecules enter them. When we exhale (this is called expiration), their volume decreases, and waste gas molecules are expelled. Our lungs cannot inflate by themselves because they do not have muscles. They expand during inhaling only when the volume of the thoracic cavity is increased through the contraction of:

the thoracic diaphragm and
intercostal muscles, which pull the rib cage outwards and upwards.

The thoracic diaphragm is a sheet muscle that separates the thoracic cavity containing lungs and heart from the abdominal cavity containing the stomach, liver, kidneys, small and large intestine, and other organs. During exhaling, the diaphragm and the intercostal muscles relax and the volume of the thoracic cavity is decreased.

The lung capacity of an average adult male is about 6 liters of air. Taller, fit people and those who live at higher altitudes have higher lung volume and shorter, obese people, and those who live at lower altitudes have smaller lung volume. Athletes have the largest lung capacity up to 12 liters. During quiet breathing, the air moved into and out of the lungs called the tidal volume is relatively small — only about 0.5 L in healthy men and 0.4 L in healthy women. At the end of each exhalation, the adult male lungs still contain 2.4 L of air, and female lungs contain 1.8 L of air. This volume is called a functional residual capacity (FRC).

Avogadro's Law Problems

It is interesting to determine how many moles and grams of air we take in and out for every respiratory cycle and what is the pressure difference that is involved in breathing. We will calculate the pressure difference that is necessary for the quiet breathing of a healthy male adult at room temperature and normal atmospheric pressure. To do this, we will use several of our calculators of ideal gas laws.

The amount of air in moles in the lungs before inhaling (FRC) is 2.4 L at 37 °C at the normal atmospheric pressure of 100 kPa is calculated using the ideal gas law (click to view the calculation in the calculator):

As we mentioned before, the tidal volume for quiet breathing in healthy men is 0.5 L. Using the Ideal Gas Calculator, we determine the amount of 0.5L of air in moles at 100 kPa and 20 °С (click to view the calculation in the calculator):

Class RDoc::Markdown RDoc::Markdown as described by the markdown syntax. To choose Markdown as your only default format see Saved Options at RDoc::Options for instructions on setting up a.docoptions file to store your project default. Usage ¶ ↑ Here is a brief example of using this parse to read a markdown file by hand. Markdown is a fantastic markup language that compiles into HTML. Although its original implementation was written in Perl, Markdown has been ported into multiple languages with various features. I use markdown for virtually any work I do. I actually wrote then entire Hello Rails course in markdown. This blog's post editor is based in markdown as well. It's safe to say I love it over any other type of word editor out there. Adding support for it in a Ruby on Rails app is quite trivial thanks to a few gems out there. The RDoc Markdown parser has the following built-in behaviors that cannot be disabled. Underscores embedded in words are never interpreted as emphasis. (While the markdown dingus emphasizes in-word underscores, neither the Markdown syntax nor MarkdownTest mention this behavior.) For HTML output, RDoc always auto-links bare URLs. Ruby markdown.

The molar mass of air is 29 g/mol, therefore the calculator shows that 0.021 mole corresponds to 0.6 g of air. Not very much, but this quantity of air in every breath is just enough to keep our body alive and well.

The temperature of the air in the lungs is 37 °C, the pressure at the end of the inspiration is the same as atmospheric pressure, therefore, according to Charles’s law, the volume of the air that entered the lungs will change to

(click to view the calculation in the calculator). The total volume of the air in the lungs of at the end of inhaling

Now we have all data to determine the pressure difference necessary for inhaling:

Air in the Lungs Characteristics	Before Inhaling	After Inhaling
Pressure of air in kPa (Pa)	100	To be determined
Temperature of air, in °C (K)	37 (310,15)	37 (310,15)
Volume of air in L (m³)	2,4 (0,0024)	2,929 (0,002929)
Quantity of air in moles	0,093	0,093 + 0,021 = 0,114

Let us determine the pressure at the start of inhaling that is necessary to inhale 0.5 L of air at 20 °C. According to the ideal gas law,

(click to view the calculation in the calculator). The pressure difference is 100.367 – 100 = 0.367 kPa = 2.75 torr = 2.75 mm Hg = 3.74 cm H₂O. This is the pressure difference between the air inside the lungs and atmospheric pressure that is necessary to inhale 0.5 L of air at normal conditions. Recall that this pressure difference is provided by the contraction of the thoracic diaphragm and intercostal muscles.